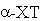Кластерная динамика гидролитических ферментов

“Задача о взаимодействии простейшего субстрата с ферментом может быть сформулирована как задача о молекуле АВ в поле нескольких лигандов” (Волькенштейн М.В., Голованов И.Б., Соболев В.М.). На примере -химотрипсина (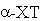) и ацетилхолинэстеразы (АХЭ) последовательно рассматриваются следующие этапы взаимодействия субстрата (АВ) с активным центром гидролитических ферментов:

а) подход АВ к входной щели активного центра (АЦ) фермента;

б) проникновение молекулы субстрата в флюктуирующую щель АЦ;

в) встречу АВ с каталитической группой (КГ) внутри АЦ и ее комплементарное связывание;

г) перестройку КГ и атаку активным атомом (ионом) КГ разрываемой связи между А и В;

д) уход продуктов реакции А и В.

На всех этапах делаются оценки статистических характеристик диффундирующих молекул АВ и молекул продуктов А и В, колебаний атомных групп, образующих входную щель АЦ, и колебаний АВ относительно активного атома КГ (атома О (Ser)), изменений длины и потенциального барьера водородной связи между атомом О (Ser) и атомом N (His).

Делается обзор соответствующих математических моделей кластерной динамики: приводится модель молекулы АХТ, состоящая из шести относительно жестких кластеров, формирующих субглобулы и АЦ АХТ; модели проникновения молекул субстрата в АЦ АХЭ и их взаимодействия с молекулами А и В; модели переноса протона в КГ АЦ АХТ и АХЭ, который определяет разрыв связи в АВ; модели колебаний молекулы субстрата, связанной вблизи КГ, необходимых для разрыва связи. Показано, что учет взаимодействия мод колебаний в 2D и 3D моделях и осцилляций параметров потенциального рельефа в АЦ со связанным субстратом способствует увеличению скорости оборота ферментов.

Работа поддержана грантами РФФИ и Центра фундаментального естествознания Минобразования РФ.

1. Romanovsky Yu. M. [1997] In: Stochastic Dynamics Eds. L. Sсhimansky-Geier, T. Poeschel. Springer Verlag, Berlin, Heidelberg, 1-13.
2. Нетребко А.В., Нетребко Н.В., Романовский Ю.М., Хургин Ю.И., Эбелинг В. [1996], Прикладная нелинейная динамика. N3, c. 54-65.
3. Нетребко А.В. и др. В настоящем сборнике.