Chlorophyll Fluorescence in vivo: A Theory (Part II).

Calculation of phytoplankton primary production.

Photosynthesis of microalgae can be measured as the rate of radioactive carbon assimilation (Steemann Nielsen, 1952) or as an increase in the concentration of soluble oxygen in a sample (Williams, 1982; Langdon, 1984). These methods are rather labor-consuming, and their application involves numerous artifacts due to prolonged isolation of phytoplankton in bottles (Eppley, 1980), difference between net and gross photosynthesis (Bender et al., 1987), and metal toxicity (Fitzwater et al., 1982). The application of chlorophyll fluorescence methods avoids these problems and allows gross photosynthesis of microalgae to be continuously measured in real time without affecting their physiological state (Kolber et al., 1990; Green et al., 1992). The relationship between chlorophyll a (Chl_a) fluorescence and photosynthesis is described in a number of biophysical models of the primary processes of photosynthesis (Weis and Berry, 1987; Genty et al.,1989; Kiefer and Reynolds, 1992).

The model of carbon assimilation V_c (mM C m^-3 s^-1) by phytoplankton is based on light dependence of photosynthesis, which can be described by a coefficient of underwater radiation absorption by photosynthetic pigments of photosystem II in suspension of microalga a_PSP (m^-1) averaged over the spectral range of underwater radiation, where PSP stands for photosynthetic pigments (Dubinsky et al., 1986), and the efficiency of the conversion of absorbed energy in photosynthetic reactions, f(I) (mM C mE^-1). The photosystems II (PS II) realize the main primary reactions of photosynthesis decomposing water and evolving oxygen.

According this assumption the photosynthesis rate is equal to:

V_c(I) = a_PSP*f(I) * I (1)

where I is the underwater radiation (mE m^-2 s^-1).

The value of f(I) is proportional to the relative number of functionally active (¦), open (q_P) reaction centers PS II in algal cells, to the efficiency of photochemical conversion of light energy in open reaction centers (fRC, mM electron mE^-1), and to the efficiency of CO₂ reduction by electrons from PS II (fe, mM C (mM electron)^-1):

V_c(I) = (a_PSP)_S*¦*q_P(I) * fRC * fe * I (2)

Assessment of ¦, f_RC and f_e:

The photochemical efficiency of open reaction center of PS II can be determined from the ratio of fluorescence parameters: fRC =(F_v/F_m)_max (Klughammer, 1992). Its known that value of fRC equal 0.83 for prevailing taxons of marine microalgae excluding blue-green algae.

It was shown that the decrease in the F_v/F_m ratio corresponds to the decrease in fraction of functioning PS II reaction centers (¦) (Kolber 1988, 90), a process which is induced by excessive irradiation (Vasiliev et al., 1994; Long et al., 1994), limitation of phytoplankton growth by mineral nutrients (Green et al., 1992; Falkowski et al., 1989) or some pollutants as heavy metals for example (Matorin, Antal, Sharshenova et al., 2001): ¦=(Fv/Fm)/(Fv/Fm)_max

Thus, parameters fRC and ¦ are proportional to the relative yield of variable fluorescence of chlorophyll in microalgae adapted to natural radiation, so we assume:

¦*fRC=F_v/F_m (3)

The value of fe was estimated from the following considerations. To reduce one molecule of CO₂, 4 electrons should be transferred from PS II , so, theoretical fe may be as high as 0.25, however, a fraction of electron flow is used for nitrate and sulfate reduction (Dubinsky et al., 1986; Laws, 1991), for cyclic electron transport around PS I (Slovacek et al., 1980; Myers, 1987) and PS II (Falkowski et al., 1986a), as well as for O₂ reduction (Chemeris, 96). This parameter couldn't be measured by fluorescence methods. Comparison of fe with the maximum quantum yield of carbon fixation allows to assume that fe is approximately constant (Kiefer et al., 1989; Morel, 1991) and is not over 0,16 for natural phytoplankton (Bannister and Wiedmann, 1984). Thus, we assume that fe =0,16.

Determination of a_PSP

The intensity of fluorescence F₀ of algae with open reaction centers (dark adapted) can be found from the equation:

F₀ = G * I_fl *(a_PSP)_fl * fFo (4)

where I_fl is the integral intensity of exciting flash (in fluorometer PrimProd I_fl(l) is nearly uniformly distributed over spectral range 400-550 nm), a constant; (a_PSP)_fl is the coefficient of fluorescence exciting flash absorption by PSP of PS II in algal suspension, averaged over spectral range 400-550 nm; fFo is the quantum yield of fluorescence in cells with open RC; G is a coefficient defined by geometric characteristics and sensitivity of the fluorescence light sensor, a constant.

Taking into account that (G * I_fl)^-1 = const, the coefficient of underwater radiation absorption by PSP of PS II of microalgae can be related to fluorescence intensity as follows:

a_PSP = const * fFo^-1 * E * F₀ = k(fFo, E) * F₀ (5)

where E = a_PSP/(a_PSP)_fl = function (depth); k is a proportionality coefficient, which equals E/fFo.

We showed that E vary from 0,7 to 0,9 in the water surface but is close to 1 in the depth 5 m and deeper. As was shown the parameter fFo is a constant for natural phytoplankton (Ostrowska et al., 2000 a,b). Thus we assume parameter k(fFo, E) as a constant.

Value of parameter k can be obtained by calibrating Fo against the coefficient of fluorescence exciting flash absorption by microalgal cells in suspension a_fl (m^-1) taken at a natural concentration (Chl_a=0.1-10 mg m^-3) (see Fig. 1). As seen from figure the dependencies almost coincide with each other for three different marine algae.

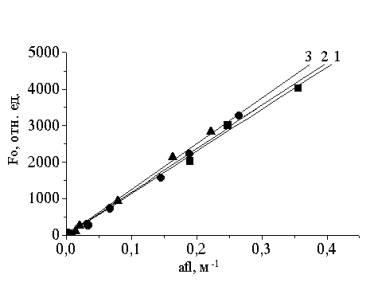
Fig. 1. Dependences Fo vs. a_fl for diatomic Th. weissflogii (square), green Ch. vulgaris (circle) and yellow-green N. salina (triangle) algae.

Determination of parameters q_p

It is known that photochemical conversion of light energy in PS II takes place only in open reaction centers. The relative concentration of open centers q_p can be found from the model of light dependent transition of reaction centers between the open (with oxidized Qa) and closed (with reduced Qa) states.

[Qa] [Qa^-][Qa] (6)

where a_RC - coefficient of light absorption by antennas of single reaction center; K - constant of Qa

oxidation rate (limiting reaction).

Making next replacements: [Qa]=q_P*[RC], [Qa^-]=(1-q_P)*[RC]

equation of reaction for q_p can be written: q_p(I)=K/(a_RCI*f_RC+K)

Replacing relation K/(a_RC*f_RC) by parameter I_1/2 we derive hyperbolic dependence:

q_p(I) = I_1/2/(I+I_1/2) (7)

where I_1/2 is light intensity, at which half of the RC are in closed state.

Value of I_1/2 can be found with accuracy assigned by variations of parameter E which increases error of measurements in the upper water (0-5 m). I_1/2 is estimated from light dependence of fluorescence obtained by pump-and-probe method (see Fig. 2).

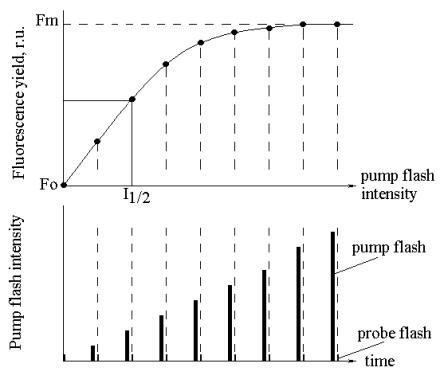
Fig. 2. Estimation of I_1/2 from dependence of fluorescence yield on pump flash intensity.

Assessment of phytoplankton photosynthesis rate per hour

By substituting 3, 5, 7, in 2 and introducing the coefficient 6.9 = 12*10^-3 (mgC (mM C)^-1) * 3600 (s h^-1) * fe, the equation for vertical profile of algae photosynthesis rate (mgC m^-3 h^-1) can be written as follows:

V_c(z) = 6.9 * k * F₀(z) * F_v/F_m(z) * I_1/2 * I(z)/(I(z)+I_1/2) (8)

where z is depth (m); k is constant for the concrete fluorometer; I_1/2 is measured in one or two water horizons. Parameters of fluorescence and underwater radiation are estimated with minimal frequency one measurement per meter of depth.